상경한 개발자 지망생들

문제 설명

GPS

카카오 택시 개발자 Jay-G는 다음 업데이트를 준비하기 위해 개선사항을 위한 여러 피드백을 받았다. 그중에서 손님이 자주 탑승하는 위치를 추천해주었으면 한다는 의견이 많았다.

다음 업데이트 준비를 위해 Jay-G는 택시의 승하차 및 이동 경로를 수집하여 분석하기 시작하였다. 데이터를 분석하던 Jay-G는 몇 가지 특이사항을 발견했다. 택시의 이동 경로를 GPS를 통해 수집하게 되는데, GPS 신호 불량, 통신 오류 등 다양한 원인으로 위치의 오류가 발생한 것을 알게 되었다. 다만 승차 위치와 하차 위치는 오류가 없는 것으로 확인이 되었다.

개발자 Jay-G는 수집한 이동 경로의 오류를 최소한으로 수정하여 좀 더 정확한 이동 경로를 구하고 싶어 한다.

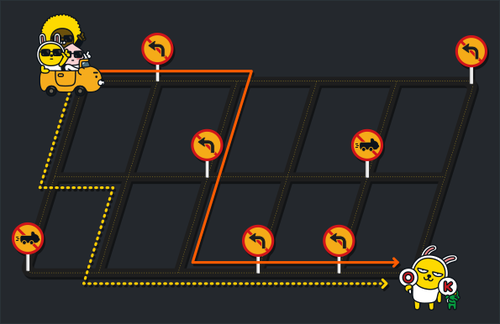
택시는 다음과 같은 조건으로만 이동한다. 먼저 택시는 거점을 이동해 다니며, 거점 간의 이동은 해당하는 도로가 있는 경우에만 가능하다. 또한, 교통 상황에 따라 택시는 한 거점에 머무를 수 있고, 왔던 길을 되돌아갈 수 있다. 모든 도로는 방향이 별도로 없는 왕복 도로이다.

예를 들어, 위 그래프에서 택시가 다음과 같이 시간대별로 이동 경로를 보내왔다.

t위치

하지만 위의 택시가 보내온 경로에는 거점 3에서 거점 6으로 이동할 수 있는 도로가 없으므로 이동 경로에 오류가 있다.

이러한 오류를 최소한으로 수정하여 이동 가능한 경로로 만들고 싶다. 이 경우 1회의 오류를 수정하여 다음과 같이 이동 가능한 경로를 만들 수 있다. 시간 t=4의 위치를 거점 5로 한 번 수정하면 이동 가능한 경로가 된다.

t위치

이와 비슷하게 시간 t=4의 위치를 거점 4로 바꾸거나, 시간 t=5 위치를 거점 5로 바꾸면 이동 가능한 경로로 만들 수 있다. 위의 경우 수정한 오류의 개수는 1개이다.

t위치

t위치

위와 같이 택시가 보내온 경로에서 이동 가능한 경로로 만드는 최소의 오류 수정 횟수를 구하여라.

입력 형식

주어지는 입력은 총 다섯 가지로, 거점 개수 n과 도로의 개수 m, 각 거점 간의 연결된 도로 정보 edge_list, 택시가 시간대별로 보내오는 거점 정보의 총 개수 k, 그리고 머물렀던 거점의 정보 gps_log이다. 제한조건은 아래와 같다.

• 2 <= n <= 200
• 1 <= m <= 10,000
• 2 <= k <= 100
• edge_list는 m × 2 크기의 2차원 배열로, 각 행의 두 값은 도로가 잇는 두 거점의 번호를 의미한다.
• 거점의 번호는 1부터 n까지 숫자이다.
• 모든 도로는 양방향 통행이 가능하다.
• 입력되는 데이터에서 항상 모든 거점 간 경로가 있음이 보장되지 않는다.
• gps_log의 시작 거점과 도착 거점은 바뀔 수 없다.

출력 형식

이동 가능한 경로로 만들 수 있는 최소의 오류 수정 횟수를 리턴한다. 올바른 경로로 수정하는 것이 불가능할 경우 -1을 리턴한다.

예제 입출력

변수명값

변수명값

예제에 대한 설명

두 예제 모두 edge_list의 데이터는 본문의 그림과 같은 예이다.
첫 번째 테스트 케이스에서 gps_log로 주어진 경로 중 거점 3에서 거점 6으로 가는 도로가 없다. 여기서 시간 t=4의 위치를 거점 5로 한 번 수정하면 이동 가능한 경로가 된다.
두 번째 테스트 케이스는 gps_log로 주어진 경로가 모두 도로로 연결된 경우이므로 수정이 필요 없다.

접근 방법

DP를 사용해 해결하였습니다. 

저는 동적계획법을 사용할 때 재귀함수를 사용한 Top-Down방식을 선호하기 때문에 Top-Down방식으로 해결하였습니다.

dp테이블의 설계는 아래와 같습니다.

dp[시간][지점] = 최적해(마지막 시간 부터 현재 시간까지의 거점들을 이동 가능 경로로 만들 수 있는 최소 변경 횟수)

 문제를 해결하기에 앞서 필요한 데이터를 전처리 해야 합니다. 저는 아래와 같은 구조로 데이터를 전처리 하였습니다.

ArrayList <ArrayList<Integer>> info = new ArrayList();

info[현재위치] = {현재 위치로 부터 갈 수 있는 거점들의 집합}

info의 초기화 코드는 아래와 같습니다.

public void init(int n, int[][] edge_list, int[] gps_log){

	this.gps_log = gps_log;
	
    //dp를 -1로 초기화
	for(int i=0;i<=gps_log.length;i++)
		Arrays.fill(dp[i], -1);

	for(int i=0;i<=n;i++){
		info.add(new ArrayList<Integer>());
		info.get(i).add(i); //정차하는 경우
	}

	for(int i=0;i<edge_list.length;i++){
		info.get(edge_list[i][0]).add(edge_list[i][1]); //양 방향
		info.get(edge_list[i][1]).add(edge_list[i][0]); //양 방향
	}
}

dp의 핵심 풀이는 info[현 위치]의 한 요소를 next라고 할 때 가능한 모든 next에 대해 최소를 구해가는 것이고, 

next == gps_log[현재 시간 + 1]라면 거점 정보의 변경 없음,  next != gps_log[현재 시간 + 1]라면 변경횟수 1회 증가를 하여 반환을 하면 됩니다. 자세한 설명은 소스 코드에 주석 처리 하겠습니다.

여기서 중요한 점은 불가능한 경우가 2가지가 있다는 점입니다.

1. edge_list에서 마지막 거점으로 가능 경로가 없는 경우

2. 마지막 거점을 변경해야지만 조건에 만족하는 경우 

소스 코드

import java.util.*;

class Solution {
    
    ArrayList <ArrayList<Integer>> info = new ArrayList();
    int[] gps_log;
    int[][] dp = new int[101][201];
    int MAX = 54321;
    
    public void init(int n, int[][] edge_list, int[] gps_log){
        
        this.gps_log = gps_log;
        
        for(int i=0;i<=gps_log.length;i++)
            Arrays.fill(dp[i], -1);
        
        for(int i=0;i<=n;i++){
            info.add(new ArrayList<Integer>());
            info.get(i).add(i); //정차하는 경우
        }
        
        for(int i=0;i<edge_list.length;i++){
            info.get(edge_list[i][0]).add(edge_list[i][1]); //양 방향
            info.get(edge_list[i][1]).add(edge_list[i][0]); //양 방향
        }
    }
    
        
    public int solve(int time, int now){
        
       	// 마지막 지점은 변경 불가능 이므로 1이 아닌 MAX를 return 
        if(time == gps_log.length - 1)
            return dp[time][now] = (gps_log[time] == now) ? 0 : MAX;
        //이미 구해진 최적해가 있다면
        if(dp[time][now] != -1)
            return dp[time][now];
        
        //ret는 최소를 구하기 위한 변수이므로 비교적 큰 값으로 초기화
        int ret = MAX;
        dp[time][now] = 0;
        
        for(int i=0;i<info.get(now).size();i++){
            int next = info.get(now).get(i);
            ret = Math.min(solve(time+1, next), ret);
        }
        
        //변경해야 하는 경우 +1
        return dp[time][now] = (gps_log[time] == now) ? ret : ret + 1;
    }
    
    public int solution(int n, int m, int[][] edge_list, int k, int[] gps_log) {
        int answer = 0;
        init(n, edge_list, gps_log);
        answer = solve(0, gps_log[0]);
        
        //마지막 지점으로 가는 경로가 없거나, 만족하는 해가 없다면
        return answer = (dp[k-1][gps_log[k-1]] == -1 || dp[k-1][gps_log[k-1]] >= MAX) ? -1 : answer;
    }
}

문제 설명

캠핑

무지를 돌보느라 지친 콘은 한적한 시골의 한 캠핑장에 놀러 갔다. 캠핑장은 텐트를 칠 수 있는 넓은 평지를 제공하고 있는데, 이 평지에는 이미 캠핑장에서 설치해 놓은 n개의 쐐기가 박혀 있다. 캠핑장 이용 고객은 이 쐐기들 중 한 쌍을 골라 다음과 같은 조건을 만족하도록 텐트를 설치해야 한다.

• 텐트는 직사각형 형태여야 한다.
• 텐트의 네 면이 정확하게 동, 서, 남, 북을 향해야 한다.
• 대각에 위치하는 텐트의 두 꼭짓점이 정확하게 선택한 두 개의 쐐기에 위치해야 한다.
• 텐트가 점유하는 직사각형 영역의 넓이는 0보다는 커야 한다.
• 텐트가 점유하는 직사각형 영역 내부에 다른 쐐기를 포함하면 안 된다. (다른 쐐기가 경계에 위치하는 경우는 허용함)

캠핑장에서는 위와 같은 조건을 만족하는 위치라면 어디든 고객이 텐트를 설치할 수 있도록 정확한 크기의 텐트를 모두 구비하여 대여해준다고 한다.
당신은 위와 같은 조건을 만족하는 텐트를 설치할 수 있는 쐐기의 쌍의 개수는 총 몇 가지가 될지 궁금해졌다.
n개의 쐐기의 위치가 좌표로 주어질 때, 위의 조건을 만족하는 쐐기의 쌍의 개수를 계산하는 프로그램을 작성하시오. 단, 동서 방향은 x축, 남북 방향은 y축과 평행하다고 가정한다.

입력 형식

입력은 쐐기의 개수를 의미하는 정수 n과, n × 2 크기의 2차원 배열 data로 주어지며, 배열의 각 행은 캠핑장에 설치된 쐐기의 x좌표와 y좌표를 의미한다. 제한 조건은 다음과 같다.

• 2 <= n <= 5,000
• n개의 쐐기는 모두 x좌표 0 이상 2^31-1 이하, y좌표 0 이상 2^31-1 이하에 위치한다.
• 입력되는 n개의 쐐기 중 x좌표와 y좌표가 모두 같은 경우는 없다.

출력 형식

입력에 주어진 각 케이스에 대해 가능한 텐트의 쐐기의 쌍의 개수를 정수 형태로 리턴한다.

예제 입출력

ndataanswer

예제에 대한 설명

예제에는 총 4개의 쐐기가 있으며 이 중 (0,0)-(1,1), (0,2)-(1,1), (1,1)-(2,0)의 세 가지 위치에만 텐트를 설치할 수 있다. (0,0)-(0,2)와 (0,0)-(2,0)의 경우에는 직사각형 영역의 넓이가 0이 되기 때문에 조건을 만족하지 못하며, (0,2)-(2,0)의 경우 (1,1) 위치의 쐐기가 직사각형의 내부에 포함되므로 조건을 만족하지 못한다.

접근 방법

 문제 풀이의 핵심은 부분합과 좌표압축입니다. 문제를 처음보았을 때 부분합은 바로 떠올랐으나 문제에서 주어지는 좌표가 너무 커 어떻게 해결해야 하나 고민을 하였습니다. 

 이 때 좌표의 값과 상관없이 좌표의 크기 순서대로 좌표를 압축한다면 부분합을 사용하여 문제를 해결할 수 있습니다.

1. 좌표 압축

저와 같은 경우는 Hash Map을 사용하여 압축을 진행하였습니다.

(만약 데이터가 [100,121,999999999999]가 있다면 [0,1,2]로 변환가능)

1. map구조에 문제에서 주어진 좌표값들을 저장을 합니다.

2. map을 for문을 사용하여 데이터를 탐색하면 자동적으로 크기가 작은 값부터 탐색이 됩니다.(Hash 함수에 의해 value가 정렬되어 있음)

3. for문을 통해 탐색을 함과 동시에 value를 압축한 값으로 저장을 합니다.

void coordCompress(vector<vector<int>> &data){
    
    map<int, int> x_mapper;
    map<int, int> y_mapper;
    
    //1. 데이터를 hashmap에 저장(x와 y는 독립적임)
    for(int i=0;i<data.size();i++){
        int x = data[i][0];
        int y = data[i][1];
        if(x_mapper.count(x) == 0)
            x_mapper.insert({x, true});
        if(y_mapper.count(y) == 0)
            y_mapper.insert({y, true});
    }
    
    //좌표 압축을 진행
    int cnt = 0;
    for(auto &elem : x_mapper){ //2. 자동적으로 value가 작은 값부터 탐색됨
        int num = elem.first;
        x_mapper[num] = cnt++; //3. 좌표압축을 진행
    }
    cnt = 0;
    for(auto &elem : y_mapper){ //2. 자동적으로 value가 작은 값부터 탐색됨
        int num = elem.first;
        y_mapper[num] = cnt++; //3. 좌표압축을 진행
    }
    
    //변환된 좌표를 벡터에 저장하지 않고 map에서 계속해서 읽어오는 것은 속도저하를 유발하므로 
    //벡터로 저장을 해야함(map은 tree구조 이므로 데이터를 탐색하는 속도가 vector보다 느림)
    for(int i=0;i<data.size();i++){
        data[i][0] = x_mapper[data[i][0]];
        data[i][1] = y_mapper[data[i][1]];
    }
    M = x_mapper.size();
    N = y_mapper.size();
}

2. 부분합

 부분합을 사용하는 이유는 선택한 두 쐐기 사이에 포함되는 쐐기를 쉽게 식별할 수 있기 때문입니다. 

부분합 arr[x][y] = {0,0} ~ {x,y}사이에 있는 쐐기의 수를 의미합니다.

void make_arr(vector<vector<int>> &data){
    
    //압축된 좌표들의 정보로 arr에 좌표를 표시
    for(int i=0;i<data.size();i++){
        int x = data[i][0];
        int y = data[i][1];
        arr[x][y] = 1;
    }
    
    // arr[x][y] = {0,0} ~ {x,y}까지 존재하는 쐐기의 수 
    //태두리의 부분합을 구함
    for(int x = 1; x < M; x++)
        arr[x][0] += arr[x - 1][0];
    for(int y = 1; y < N; y++)
        arr[0][y] += arr[0][y - 1];
    
    //내부의 부분합을 구함
    for(int x = 1; x < M; x++){
        for(int y = 1; y < N; y++){
            arr[x][y] += arr[x - 1][y] + arr[x][y - 1] - arr[x - 1][y - 1];
        }    
    }
}

위의 과정 까지 진행했다면 2개의 쐐기를 선택하는 모든 경우에 대해 3가지 조건을 검사합니다.

1. 두 쐐기의 x좌표가 같은지

2. 두 쐐기의 y좌표가 같은지

3. 두 쐐기 사이에 다른 쐐기가 있는지(태두리에 쐐기가 있는 것은 무관함)

int solve(vector<vector<int>> &data){
    
    int cnt = 0;
    
    for(int i = 0; i < data.size(); i++){
        for(int j = i + 1; j < data.size(); j++){
            
            int h_x = max(data[i][0], data[j][0]);
            int h_y = max(data[i][1], data[j][1]);
            int l_x = min(data[i][0], data[j][0]);
            int l_y = min(data[i][1], data[j][1]);
            
            //x가 같거나, y가 같거나, 사이에 쐐기가 있는 경우
            if(h_x == l_x || h_y == l_y || 0 < arr[h_x - 1][h_y - 1] - arr[h_x - 1][l_y] - arr[l_x][h_y - 1] + arr[l_x][l_y])
                continue;  
            cnt++;
        }    
    }
    return cnt;
}

소스 코드

#include <vector>
#include <string.h>
#include <iostream>
#include <map>

using namespace std;

int arr[5001][5001];
int M, N;

void coordCompress(vector<vector<int>> &data){
    
    map<int, int> x_mapper;
    map<int, int> y_mapper;
    
    for(int i=0;i<data.size();i++){
        int x = data[i][0];
        int y = data[i][1];
        if(x_mapper.count(x) == 0)
            x_mapper.insert({x, true});
        if(y_mapper.count(y) == 0)
            y_mapper.insert({y, true});
    }
    
    int cnt = 0;
    for(auto &elem : x_mapper){
        int num = elem.first;
        x_mapper[num] = cnt++;
    }
    cnt = 0;
    for(auto &elem : y_mapper){
        int num = elem.first;
        y_mapper[num] = cnt++;
    }
    
    for(int i=0;i<data.size();i++){
        data[i][0] = x_mapper[data[i][0]];
        data[i][1] = y_mapper[data[i][1]];
    }
    M = x_mapper.size();
    N = y_mapper.size();
}

void make_arr(vector<vector<int>> &data){
    
    for(int i=0;i<data.size();i++){
        int x = data[i][0];
        int y = data[i][1];
        arr[x][y] = 1;
    }
    
    for(int x = 1; x < M; x++)
        arr[x][0] += arr[x - 1][0];
    for(int y = 1; y < N; y++)
        arr[0][y] += arr[0][y - 1];
    
    for(int x = 1; x < M; x++){
        for(int y = 1; y < N; y++){
            arr[x][y] += arr[x - 1][y] + arr[x][y - 1] - arr[x - 1][y - 1];
        }    
    }
}

int solve(vector<vector<int>> &data){
    
    int cnt = 0;
    
    for(int i = 0; i < data.size(); i++){
        for(int j = i + 1; j < data.size(); j++){
            
            int h_x = max(data[i][0], data[j][0]);
            int h_y = max(data[i][1], data[j][1]);
            int l_x = min(data[i][0], data[j][0]);
            int l_y = min(data[i][1], data[j][1]);
            
            //x가 같거나, y가 같거나, 사이에 쐐기가 있는 경우
            if(h_x == l_x || h_y == l_y || 0 < arr[h_x - 1][h_y - 1] - arr[h_x - 1][l_y] - arr[l_x][h_y - 1] + arr[l_x][l_y])
                continue;  
            cnt++;
        }    
    }
    return cnt;
}

// 전역 변수를 정의할 경우 함수 내에 초기화 코드를 꼭 작성해주세요.
int solution(int n, vector<vector<int>> data) {
    
    int answer = 0;
    memset(arr, 0, sizeof(arr));
    M = 0; N = 0;
    
    coordCompress(data);
    make_arr(data);
    
    answer = solve(data);
    return answer;
}

문제 설명

문제 설명

출발지점부터 distance만큼 떨어진 곳에 도착지점이 있습니다. 그리고 그사이에는 바위들이 놓여있습니다. 바위 중 몇 개를 제거하려고 합니다.
예를 들어, 도착지점이 25만큼 떨어져 있고, 바위가 [2, 14, 11, 21, 17] 지점에 놓여있을 때 바위 2개를 제거하면 출발지점, 도착지점, 바위 간의 거리가 아래와 같습니다.

제거한 바위의 위치각 바위 사이의 거리거리의 최솟값

위에서 구한 거리의 최솟값 중에 가장 큰 값은 4입니다.

출발지점부터 도착지점까지의 거리 distance, 바위들이 있는 위치를 담은 배열 rocks, 제거할 바위의 수 n이 매개변수로 주어질 때, 바위를 n개 제거한 뒤 각 지점 사이의 거리의 최솟값 중에 가장 큰 값을 return 하도록 solution 함수를 작성해주세요.

제한사항

• 도착지점까지의 거리 distance는 1 이상 1,000,000,000 이하입니다.
• 바위는 1개 이상 50,000개 이하가 있습니다.
• n 은 1 이상 바위의 개수 이하입니다.

입출력 예

distancerocksnreturn

접근 방법

 꽤 난이도가 있는 이분탐색 문제였습니다.

1. 문제 풀이의 핵심은 mid를 "거리의 최소값"으로 생각하고 징검다리를 순차적으로 최대 n개까지 제거해보며 모두 간격이 mid보다 넓은지 확인하는 것이다. 

2-1. 만약 mid보다 좁은 간격이라면 다음 징검다리를 제거하고 다음 징검다리까지의 간격을 확인합니다. (최대 n번까지 가능)

2-2. 만약 n개의 징검다리를 제거 했음에도 mid보다 좁은 간격의 징검다리가 존재한다면 mid는 만족할 수 없음으로 mid를 줄여 조정합니다. 

3. 만약 mid와 같거나 넓은 간격이라면 mid를 증가시켜보며 mid의 최댓값을 구합니다.

소스 코드

#include <string>
#include <vector>
#include <algorithm>

using namespace std;

vector<int> diffs; //간격을 저장한 벡터

void init(vector<int> &rocks, int dist){
    
    sort(rocks.begin(), rocks.end());
    
    int start = 0;
    for(int i=0;i<rocks.size();i++){
        int diff = rocks[i] - start;
        diffs.push_back(diff);
        start = rocks[i];
    }
    diffs.push_back(dist - rocks.back());
}

int bSearch(int distance, int n){
    
    int start = 1;
    int end = distance;
    int result = 0;
    
    while(start <= end){
        
        int mid = (start + end) / 2;
        int removeCnt = 0; //제거한 징검다리의 수
        int prevDist = 0; //징검다리를 제거하였을 때 연장되는 길이를 저장한 값
        
        //모든 간격이 mid보다 넓은지 확인하는 과정
        for(int i=0;i<diffs.size();i++){
            if(mid > diffs[i] + prevDist){ //징검다리를 제거해야 하는 경우
                prevDist += diffs[i];
                removeCnt++;
            }
            else{ //징검다리를 제거하지 않고 만족하는 경우
                prevDist = 0;
            }
            if(removeCnt > n)
                break;
        }
        
        if(removeCnt > n){
            end = mid - 1;
        }
        else{
            result = (result == 0) ? mid : max(mid, result);
            start = mid + 1;
        }
    }
    return result;
}

int solution(int distance, vector<int> rocks, int n) {
    
    int answer = 0;
    init(rocks, distance);
    
    return answer = bSearch(distance, n);
}

문제 설명

문제 설명

n명이 입국심사를 위해 줄을 서서 기다리고 있습니다. 각 입국심사대에 있는 심사관마다 심사하는데 걸리는 시간은 다릅니다.

처음에 모든 심사대는 비어있습니다. 한 심사대에서는 동시에 한 명만 심사를 할 수 있습니다. 가장 앞에 서 있는 사람은 비어 있는 심사대로 가서 심사를 받을 수 있습니다. 하지만 더 빨리 끝나는 심사대가 있으면 기다렸다가 그곳으로 가서 심사를 받을 수도 있습니다.

모든 사람이 심사를 받는데 걸리는 시간을 최소로 하고 싶습니다.

입국심사를 기다리는 사람 수 n, 각 심사관이 한 명을 심사하는데 걸리는 시간이 담긴 배열 times가 매개변수로 주어질 때, 모든 사람이 심사를 받는데 걸리는 시간의 최솟값을 return 하도록 solution 함수를 작성해주세요.

제한사항

• 입국심사를 기다리는 사람은 1명 이상 1,000,000,000명 이하입니다.
• 각 심사관이 한 명을 심사하는데 걸리는 시간은 1분 이상 1,000,000,000분 이하입니다.
• 심사관은 1명 이상 100,000명 이하입니다.

입출력 예

ntimesreturn

입출력 예 설명

가장 첫 두 사람은 바로 심사를 받으러 갑니다.

7분이 되었을 때, 첫 번째 심사대가 비고 3번째 사람이 심사를 받습니다.

10분이 되었을 때, 두 번째 심사대가 비고 4번째 사람이 심사를 받습니다.

14분이 되었을 때, 첫 번째 심사대가 비고 5번째 사람이 심사를 받습니다.

20분이 되었을 때, 두 번째 심사대가 비지만 6번째 사람이 그곳에서 심사를 받지 않고 1분을 더 기다린 후에 첫 번째 심사대에서 심사를 받으면 28분에 모든 사람의 심사가 끝납니다.

접근 방법

 이분탐색을 활용하여 풀 수 있는 재미있는 문제였습니다.

이분탐색에서의 mid를 모든 사람을 심사하는데 걸리는 시간으로 잡고 최소가 되는 mid를 구하면 됩니다. 

 mid초 일 때 심사 할 수 있는 인원을 계산하는 방법은 각 인원(times[i])이 mid초 동안 몇 명을 심사할 수 있는지 계산하여 합하면 구할 수 있습니다. (심사한 인원 = times[i] / mid )

 이 때 mid초 동안 총 심사한 인원이 cnt명이라 할 때 cnt < n이면 더욱 많은 시간이 소요된다는 의미이고, 그 반대의 경우는 mid초 동안 n명을 모두 심사할 수 있다는 의미가 됩니다. 

즉 cnt >= n인 경우를 만족하는 mid중 최솟 값이 정답이 됩니다.

소스 코드

#include <string>
#include <vector>
#include <algorithm>
#include <iostream>

using namespace std;

vector<long long> v;

long long bSearch(int n, vector<int> &times){
    
    sort(times.begin(), times.end());
    
    long long start = 1;
    long long end = times.back() * (long long)n;
    long long result = 0;
    
    while(start <= end){
        
        long long mid = (start + end)/2;
        
        long long cnt = 0;
        for(int i=0;i<times.size();i++){
            cnt += mid / times[i]; //mid시간 동안 처리할 수 있는 사람의 수 
        }
        
        if(cnt < n){ //시간내로 처리 불가능, 처리시간 증가 요구
            start = mid + 1;
        }
        else{
            result = (result == 0) ? mid : min(result, mid);
            end = mid - 1;
        }
    }
    return result;
}

long long solution(int n, vector<int> times) {
    long long answer = 0;
    return answer = bSearch(n, times); 
}

문제 설명

보행자 천국

카카오내비 개발자인 제이지는 시내 중심가의 경로 탐색 알고리즘 개발 업무를 담당하고 있다. 최근 들어 보행자가 자유롭고 편리하게 걸을 수 있도록 보행자 중심의 교통 체계가 도입되면서 도심의 일부 구역은 자동차 통행이 금지되고, 일부 교차로에서는 보행자 안전을 위해 좌회전이나 우회전이 금지되기도 했다. 복잡해진 도로 환경으로 인해 기존의 경로 탐색 알고리즘을 보완해야 할 필요가 생겼다.

도시 중심가의 지도는 m × n 크기의 격자 모양 배열 city_map으로 주어진다. 자동차는 오른쪽 또는 아래 방향으로 한 칸씩 이동 가능하다.

city_map[i][j]에는 도로의 상황을 나타내는 값이 저장되어 있다.

• 0인 경우에는 자동차가 자유롭게 지나갈 수 있다.
• 1인 경우에는 자동차 통행이 금지되어 지나갈 수 없다.
• 2인 경우는 보행자 안전을 위해 좌회전이나 우회전이 금지된다. (왼쪽에서 오던 차는 오른쪽으로만, 위에서 오던 차는 아래쪽으로만 진행 가능하다)

도시의 도로 상태가 입력으로 주어졌을 때, 왼쪽 위의 출발점에서 오른쪽 아래 도착점까지 자동차로 이동 가능한 전체 가능한 경로 수를 출력하는 프로그램을 작성하라. 이때 가능한 경로의 수는 컴퓨터가 표현할 수 있는 정수의 범위를 넘어설 수 있으므로, 가능한 경로 수를 20170805로 나눈 나머지 값을 출력하라.

입력 형식

입력은 도시의 크기를 나타내는 m과 n, 그리고 지도를 나타내는 2차원 배열 city_map으로 주어진다. 제한조건은 아래와 같다.

• 1 <= m, n <= 500
• city_map의 크기는 m × n이다.
• 배열의 모든 원소의 값은 0, 1, 2 중 하나이다.
• 출발점의 좌표는 (0, 0), 도착점의 좌표는 (m - 1, n - 1)이다.
• 출발점과 도착점의 city_map[i][j] 값은 0이다.

출력 형식

출발점에서 도착점까지 이동 가능한 전체 경로의 수를 20170805로 나눈 나머지를 리턴한다.

예제 입출력

mncity_mapanswer

예제에 대한 설명

첫 번째 예제는 모든 도로가 제한 없이 통행 가능한 경우로, 가능한 경우의 수는 6가지이다.
두 번째 예제는 문제 설명에 있는 그림의 경우이다. 가능한 경우의 수는 빨간 실선과 노란 점선 2가지뿐이다.

접근 방법

 동적계획법으로 해결할 수 있는 문제였습니다. 동적계획법은 dp[x좌표][y좌표][현재방향]으로 설계할 수 있으며 현재방향에 대한 차원이 필요한 이유는 만약 어떤 지점의 값이 2일때 한 방향으로만 갈 수 있으므로 현재 어떤 방향을 가지고 있는가에 따라 다른 경우의 수가 되기 때문입니다. 

 자세한 내용은 코드에 주석을 달아놓겠습니다.

소스 코드

#include <vector>
#include <string.h>

using namespace std;

int MOD = 20170805;
int dp[501][501][2]; //마지막 차원은 현재 방향
pair<int, int> nextdir[2] = {{1,0},{0,1}}; //오른쪽 또는 아래로만 이동 가능
vector<vector<int>> map;
int M, N;

bool inRange(int x, int y){
    return (0 <= x && x < M && 0 <= y && y < N);
}

int solve(int x, int y, int dir){
    
    int &ref = dp[x][y][dir];
    
    //방문한 적 있다면
    if(ref != -1)
        return ref;
    //목표지점에 도달했다면
    if(x == M - 1 && y == N - 1)
        return ref = 1;
    
    //방문 표시
    ref = 0;
    //2방향 모두 가능
    if(map[x][y] != 2){
        
        //2방향에 대한 반복문
        for(int i=0;i<2;i++){
            int next_x = x + nextdir[i].first;
            int next_y = y + nextdir[i].second;
            //다음 좌표가 범위를 벗어나지 않으며 통행 불가 지역이 아닌 경우
            if(inRange(next_x, next_y) && map[next_x][next_y] != 1)
                ref += solve(next_x, next_y, i) % MOD;     
        }    
    }
    else{ //회전 불가능, map[x][y] == 2인 경우
        //현재 진행 방향이 dir이며 dir로만 진행 가능
        int next_x = x + nextdir[dir].first;
        int next_y = y + nextdir[dir].second;
        if(inRange(next_x, next_y) && map[next_x][next_y] != 1)
            ref += solve(next_x, next_y, dir) % MOD;     
    }
    return ref %= MOD;
}

// 전역 변수를 정의할 경우 함수 내에 초기화 코드를 꼭 작성해주세요.
int solution(int m, int n, vector<vector<int>> city_map) {
    
    int answer = 0;
    memset(dp, -1, sizeof(dp));
    //전역 변수로 초기화
    M = m; N = n; map = city_map;
    
    return answer = solve(0, 0, 0);
}

문제 설명

N x N 크기인 정사각 격자 형태의 지형이 있습니다. 각 격자 칸은 1 x 1 크기이며, 숫자가 하나씩 적혀있습니다. 격자 칸에 적힌 숫자는 그 칸의 높이를 나타냅니다.

이 지형의 아무 칸에서나 출발해 모든 칸을 방문하는 탐험을 떠나려 합니다. 칸을 이동할 때는 상, 하, 좌, 우로 한 칸씩 이동할 수 있는데, 현재 칸과 이동하려는 칸의 높이 차가 height 이하여야 합니다. 높이 차가 height 보다 많이 나는 경우에는 사다리를 설치해서 이동할 수 있습니다. 이때, 사다리를 설치하는데 두 격자 칸의 높이차만큼 비용이 듭니다. 따라서, 최대한 적은 비용이 들도록 사다리를 설치해서 모든 칸으로 이동 가능하도록 해야 합니다. 설치할 수 있는 사다리 개수에 제한은 없으며, 설치한 사다리는 철거하지 않습니다.

각 격자칸의 높이가 담긴 2차원 배열 land와 이동 가능한 최대 높이차 height가 매개변수로 주어질 때, 모든 칸을 방문하기 위해 필요한 사다리 설치 비용의 최솟값을 return 하도록 solution 함수를 완성해주세요.

제한사항

• land는 N x N크기인 2차원 배열입니다.
• land의 최소 크기는 4 x 4, 최대 크기는 300 x 300입니다.
• land의 원소는 각 격자 칸의 높이를 나타냅니다.
• 격자 칸의 높이는 1 이상 10,000 이하인 자연수입니다.
• height는 1 이상 10,000 이하인 자연수입니다.

입출력 예

landheightresult

입출력 예 설명

입출력 예 #1

각 칸의 높이는 다음과 같으며, 높이차가 3 이하인 경우 사다리 없이 이동이 가능합니다.

위 그림에서 사다리를 이용하지 않고 이동 가능한 범위는 같은 색으로 칠해져 있습니다. 예를 들어 (1행 2열) 높이 4인 칸에서 (1행 3열) 높이 8인 칸으로 직접 이동할 수는 없지만, 높이가 5인 칸을 이용하면 사다리를 사용하지 않고 이동할 수 있습니다.

따라서 다음과 같이 사다리 두 개만 설치하면 모든 칸을 방문할 수 있고 최소 비용은 15가 됩니다.

• 높이 5인 칸 → 높이 10인 칸 : 비용 5
• 높이 10인 칸 → 높이 20인 칸 : 비용 10

입출력 예 #2

각 칸의 높이는 다음과 같으며, 높이차가 1 이하인 경우 사다리 없이 이동이 가능합니다.

위 그림과 같이 (2행 1열) → (1행 1열), (1행 2열) → (2행 2열) 두 곳에 사다리를 설치하면 설치비용이 18로 최소가 됩니다.

접근 방법

 최소 신장 트리 알고리즘을 알고 있다면 크게 생각할 부분이 없는 문제였습니다. 

 최소 신장 트리는 모든 노드를 연결하였을 때 드는 간선의 최소 비용을 구하는 알고리즘입니다. 그러므로 문제에서 모든 칸을 이동할 수 있도록 사다리를 설치해야 한다는 점과 사다리의 설치 비용의 최소가 된다는 점을 본다면 MST(최소 신장 트리)를 바로 떠올릴 수 있습니다. 

사다리 설치가 없는 지역간의 이동 비용은 0, 사다리를 설치해야하는 지역간의 이동 비용은 인접한 격자 값의 차이가 될 것입니다. 

유의할 점으로 최소 신장 트리를 구성할 때 노드 번호를 격자의 좌표인 2차원 좌표로 표현하였습니다.

소스 코드

#include <string>
#include <vector>
#include <cmath>
#include <algorithm>

using namespace std;

typedef struct coord{
    int x, y;
};
typedef struct info{
    coord now, next;
    int cost;
};

vector<info> costmap;
pair<int, int> nextdir[2] = {{1,0},{0,1}};
coord parent[301][301];

bool comp(info &a, info &b){
    return a.cost < b.cost;
}

void make_costmap(vector<vector<int>> &land, int h){
    
    for (int i = 0; i < land.size(); i++) 
        for (int j = 0; j < land.size(); j++) 
            parent[i][j] = {i,j};    
    
    for(int i=0;i<land.size();i++){
        for(int j=0;j<land.size();j++){
            for(int dir=0;dir<2;dir++){
                int next_x = i + nextdir[dir].first;
                int next_y = j + nextdir[dir].second;
                if(0 <= next_x && next_x < land.size() && 0 <= next_y && next_y < land.size()){
                    if(abs(land[i][j] - land[next_x][next_y]) <= h) costmap.push_back({{i,j},{next_x, next_y}, 0});
                    else costmap.push_back({{i,j},{next_x, next_y}, abs(land[i][j] - land[next_x][next_y])});
                }
            }
        }    
    }
}

coord find(coord a) {
	if (parent[a.x][a.y].x == a.x && parent[a.x][a.y].y == a.y) {
		return a;
	}
	coord root = find(parent[a.x][a.y]);
	return root;
}

bool Union(coord a, coord b) {
	a = find(a);
	b = find(b);
	if (a.x != b.x || a.y != b.y) {
		parent[b.x][b.y] = a;
		return true;
	}
	return false;
}

int solve(){
    
    sort(costmap.begin(), costmap.end(), comp);
    
    int result = 0;
	for (int i = 0; i < costmap.size(); i++) {
		if (Union(costmap[i].now, costmap[i].next)) 
			result += costmap[i].cost;
	}
    return result;
}

int solution(vector<vector<int>> land, int height) {
    int answer = 0;
    make_costmap(land, height);
    return answer = solve();
}

문제 설명

블록게임

프렌즈 블록이라는 신규 게임이 출시되었고, 어마어마한 상금이 걸린 이벤트 대회가 개최 되었다.

이 대회는 사람을 대신해서 플레이할 프로그램으로 참가해도 된다는 규정이 있어서, 게임 실력이 형편없는 프로도는 프로그램을 만들어서 참가하기로 결심하고 개발을 시작하였다.

프로도가 우승할 수 있도록 도와서 빠르고 정확한 프로그램을 작성해 보자.

게임규칙

아래 그림과 같이 1×1 크기의 블록을 이어 붙여 만든 3 종류의 블록을 회전해서 총 12가지 모양의 블록을 만들 수 있다.

1 x 1 크기의 정사각형으로 이루어진 N x N 크기의 보드 위에 이 블록들이 배치된 채로 게임이 시작된다. (보드 위에 놓인 블록은 회전할 수 없다). 모든 블록은 블록을 구성하는 사각형들이 정확히 보드 위의 사각형에 맞도록 놓여있으며, 선 위에 걸치거나 보드를 벗어나게 놓여있는 경우는 없다.

플레이어는 위쪽에서 1 x 1 크기의 검은 블록을 떨어뜨려 쌓을 수 있다. 검은 블록은 항상 맵의 한 칸에 꽉 차게 떨어뜨려야 하며, 줄에 걸치면 안된다.
이때, 검은 블록과 기존에 놓인 블록을 합해 속이 꽉 채워진 직사각형을 만들 수 있다면 그 블록을 없앨 수 있다.

예를 들어 검은 블록을 떨어뜨려 아래와 같이 만들 경우 주황색 블록을 없앨 수 있다.

빨간 블록을 가로막던 주황색 블록이 없어졌으므로 다음과 같이 빨간 블록도 없앨 수 있다.

그러나 다른 블록들은 검은 블록을 떨어뜨려 직사각형으로 만들 수 없기 때문에 없앨 수 없다.

따라서 위 예시에서 없앨 수 있는 블록은 최대 2개이다.

보드 위에 놓인 블록의 상태가 담긴 2차원 배열 board가 주어질 때, 검은 블록을 떨어뜨려 없앨 수 있는 블록 개수의 최댓값을 구하라.

제한사항

• board는 블록의 상태가 들어있는 N x N 크기 2차원 배열이다.
  • N은 4 이상 50 이하다.
• board의 각 행의 원소는 0 이상 200 이하의 자연수이다.
  • 0 은 빈 칸을 나타낸다.
  • board에 놓여있는 각 블록은 숫자를 이용해 표현한다.
  • 잘못된 블록 모양이 주어지는 경우는 없다.
  • 모양에 관계 없이 서로 다른 블록은 서로 다른 숫자로 표현된다.
  • 예를 들어 문제에 주어진 예시의 경우 다음과 같이 주어진다.

접근 방법

특별하게 사용할 알고리즘이 따로 생각나지 않는 시뮬레이션 문제였습니다.

접근 방법은 아래와 같습니다.

1. board의 전체에 1개씩 검은 블록을 떨어트린다.

2. 제거 할 수 있는 블록이 있는지 확인한다. 제거할 수 있는 블록이 있다면 제거한다.

3. 2에서 블록이 제거 되었다면 board에 남아있는 모든 검은 블록을 제거한다. 어떤 블록도 제거되지 않았다면 놔둔다.

4. 1번부터 반복 (만약 3번 연속 블록이 제거되지 않았다면 더 이상 제거할 블록이 없다는 것이므로 반복을 종료한다.)

int solve(vector<vector<int>> &board){
    
    int total = 0;
    int zeroCnt = 0;
    
    while(zeroCnt < 3){
        
        stackBlack(board); //1번: 검은 블록을 전체에 떨어트림
        int cnt = check(board); //2번: 제거 할 수 있는 블록을 count
        
        //3번
        if(cnt == 0) 
            zeroCnt++;
        else{
            eraseBlack(board);
            zeroCnt = 0;  
        } 
        
        total += cnt;    
    }
    
    return total;
}

1. board의 전체에 1개씩 검은 블록을 떨어트린다.

한 열의 가장 위 부터 확인하며 어떤 블록이 발견되면 검은 블록을 쌓습니다. 저와 같은 경우 검은 블록은 -1로 표기 하였습니다. 이 때 주의할 점은 블록이 board의 최상단까지 쌓여있다면 다음 열로 넘어가야 한다는 것입니다.

void stackBlack(vector<vector<int>> &board){
    
    for(int i=0;i<board.size();i++){ //i가 가로
        for(int j=0;j<board[i].size();j++){ //j가 높이
            if(board[j][i] != 0){
                if(j == 0) //보드의 가장 위에 블록이 있다면
                    break;
                board[j - 1][i] = -1;
                break;
            }
        }    
    }
}

2. 제거 할 수 있는 블록이 있는지 확인한다. 제거할 수 있는 블록이 있다면 제거한다.

 일단 board의 처음부터 끝까지 한 칸씩 스캔을 하다 어떤 블록이 발견되면 그 위치에서 제거할 수 있는 블록이 있는지 확인을 합니다. 이 때 제거할 수 있는 블록의 형태는 3x2또는 2x3이므로 두 가지 형태에 대해 검사를 합니다.

int check(vector<vector<int>> &board){
    
    int cnt = 0;
    
    for(int i=0;i<board.size();i++)
        for(int j=0;j<board.size();j++)
            if(board[i][j] != 0)
                if(checkOneArea(i,j,2,3,board) || checkOneArea(i,j,3,2,board)) // 2*3모양 3*2모양에 대해서만 확인하면 됨
                    cnt++;       
    
    return cnt;
}

checkOneArea()함수에서는 매개변수로 확인해야할 지점과 범위를 매개변수로 주어 제거할 수 있는 블록이 있다면 제거를 한뒤 true를 반환하고, 제거할 수 있는 블록이 없다면 false를 반환합니다.

 이 때 제거할 수 있는 블록의 조건으로는 모든 기본 블록은 4개로 이루어져 있기 때문에 검은블록(-1)이 무조건 2개만 포함이 되어야 한다는 것이고 검은 블록과 제거할 블록의 색 외에 다른 어떠한 색도 포함이 되면 안된다는 것입니다.

bool checkOneArea(int x, int y, int x_len, int y_len, vector<vector<int>> &board){
    
    int color = 0;
    int blackCnt = 0;
    
    //검사 범위를 벗어나는 경우
    if(board.size() < x + x_len || board.size() < y + y_len) 
        return false;
    
    for(int i = x; i < x + x_len; i++){
        for(int j = y; j < y + y_len; j++){
            if(board[i][j] == 0)
                return false;
            if(board[i][j] == -1)
                blackCnt++;
            if(board[i][j] != -1 && color == 0) //검은 블록이 아닌 블록의 색을 color에 지정
                color = board[i][j];
            if(board[i][j] != -1 && board[i][j] != color) //지정된 color와 다른 색이라면 제거 불가능
                return false;
        }    
    }
    
    if(blackCnt != 2) 
        return false;
    
    //블록 제거
    for(int i = x; i < x + x_len; i++)
        for(int j = y; j < y + y_len; j++)
            board[i][j] = 0;
    
    return true;
}

3번과 4번의 과정은 간단하므로 자세한 설명은 생략하겠습니다.

소스 코드

#include <string>
#include <vector>

using namespace std;

void stackBlack(vector<vector<int>> &board){
    
    for(int i=0;i<board.size();i++){ //i가 가로
        for(int j=0;j<board[i].size();j++){ //j가 높이
            if(board[j][i] != 0){
                if(j == 0)
                    break;
                board[j - 1][i] = -1;
                break;
            }
        }    
    }
}

bool checkOneArea(int x, int y, int x_len, int y_len, vector<vector<int>> &board){
    
    int color = 0;
    int blackCnt = 0;
    
    //검사범위를 벗어나는 경우
    if(board.size() < x + x_len || board.size() < y + y_len) 
        return false;
    
    for(int i = x; i < x + x_len; i++){
        for(int j = y; j < y + y_len; j++){
            if(board[i][j] == 0)
                return false;
            if(board[i][j] == -1)
                blackCnt++;
            if(board[i][j] != -1 && color == 0) //검은 블록이 아닌 블록의 색을 color에 지정
                color = board[i][j];
            if(board[i][j] != -1 && board[i][j] != color) //지정된 color와 다른 색이라면 제거 불가능
                return false;
        }    
    }
    
    if(blackCnt != 2) 
        return false;
    
    //블록 제거
    for(int i = x; i < x + x_len; i++)
        for(int j = y; j < y + y_len; j++)
            board[i][j] = 0;
    
    return true;
}

int check(vector<vector<int>> &board){
    
    int cnt = 0;
    
    for(int i=0;i<board.size();i++)
        for(int j=0;j<board.size();j++)
            if(board[i][j] != 0)
                if(checkOneArea(i,j,2,3,board) || checkOneArea(i,j,3,2,board)) // 2*3모양 3*2모양에 대해서만 확인하면 됨
                    cnt++;       
    
    return cnt;
}

void eraseBlack(vector<vector<int>> &board){
    
    for(int i=0;i<board.size();i++)
        for(int j=0;j<board.size();j++)
            if(board[i][j] == -1)
                board[i][j] = 0;
}

int solve(vector<vector<int>> &board){
    
    int total = 0;
    int zeroCnt = 0;
    
    while(zeroCnt < 3){
        
        stackBlack(board); //검은 블록을 전체에 떨어트림
        int cnt = check(board); //제거 할 수 있는 블록을 count
        
        if(cnt == 0)
            zeroCnt++;
        else{
            eraseBlack(board);
            zeroCnt = 0;  
        } 
        
        total += cnt;    
    }
    
    return total;
}

int solution(vector<vector<int>> board) {
    
    int answer = solve(board);
    return answer;
}

문제 설명

매칭 점수

프렌즈 대학교 조교였던 제이지는 허드렛일만 시키는 네오 학과장님의 마수에서 벗어나, 카카오에 입사하게 되었다.
평소에 관심있어하던 검색에 마침 결원이 발생하여, 검색개발팀에 편입될 수 있었고, 대망의 첫 프로젝트를 맡게 되었다.
그 프로젝트는 검색어에 가장 잘 맞는 웹페이지를 보여주기 위해 아래와 같은 규칙으로 검색어에 대한 웹페이지의 매칭점수를 계산 하는 것이었다.

• 한 웹페이지에 대해서 기본점수, 외부 링크 수, 링크점수, 그리고 매칭점수를 구할 수 있다.
• 한 웹페이지의 기본점수는 해당 웹페이지의 텍스트 중, 검색어가 등장하는 횟수이다. (대소문자 무시)
• 한 웹페이지의 외부 링크 수는 해당 웹페이지에서 다른 외부 페이지로 연결된 링크의 개수이다.
• 한 웹페이지의 링크점수는 해당 웹페이지로 링크가 걸린 다른 웹페이지의 기본점수 ÷ 외부 링크 수의 총합이다.
• 한 웹페이지의 매칭점수는 기본점수와 링크점수의 합으로 계산한다.

예를 들어, 다음과 같이 A, B, C 세 개의 웹페이지가 있고, 검색어가 hi라고 하자.

이때 A 웹페이지의 매칭점수는 다음과 같이 계산할 수 있다.

• 기본 점수는 각 웹페이지에서 hi가 등장한 횟수이다.
  • A,B,C 웹페이지의 기본점수는 각각 1점, 4점, 9점이다.
• 외부 링크수는 다른 웹페이지로 링크가 걸린 개수이다.
  • A,B,C 웹페이지의 외부 링크 수는 각각 1점, 2점, 3점이다.
• A 웹페이지로 링크가 걸린 페이지는 B와 C가 있다.
  • A 웹페이지의 링크점수는 B의 링크점수 2점(4 ÷ 2)과 C의 링크점수 3점(9 ÷ 3)을 더한 5점이 된다.
• 그러므로, A 웹페이지의 매칭점수는 기본점수 1점 + 링크점수 5점 = 6점이 된다.

검색어 word와 웹페이지의 HTML 목록인 pages가 주어졌을 때, 매칭점수가 가장 높은 웹페이지의 index를 구하라. 만약 그런 웹페이지가 여러 개라면 그중 번호가 가장 작은 것을 구하라.

제한사항

• pages는 HTML 형식의 웹페이지가 문자열 형태로 들어있는 배열이고, 길이는 1 이상 20 이하이다.
• 한 웹페이지 문자열의 길이는 1 이상 1,500 이하이다.
• 웹페이지의 index는 pages 배열의 index와 같으며 0부터 시작한다.
• 한 웹페이지의 url은 HTML의 <head> 태그 내에 <meta> 태그의 값으로 주어진다.
  • 예를들어, 아래와 같은 meta tag가 있으면 이 웹페이지의 url은 https://careers.kakao.com/index 이다.
  • <meta property=og:url content=https://careers.kakao.com/index />
• 한 웹페이지에서 모든 외부 링크는 <a href=https://careers.kakao.com/index>의 형태를 가진다.
  • <a> 내에 다른 attribute가 주어지는 경우는 없으며 항상 href로 연결할 사이트의 url만 포함된다.
  • 위의 경우에서 해당 웹페이지는 https://careers.kakao.com/index 로 외부링크를 가지고 있다고 볼 수 있다.
• 모든 url은 https:// 로만 시작한다.
• 검색어 word는 하나의 영어 단어로만 주어지며 알파벳 소문자와 대문자로만 이루어져 있다.
• word의 길이는 1 이상 12 이하이다.
• 검색어를 찾을 때, 대소문자 구분은 무시하고 찾는다.
  • 예를들어 검색어가 blind일 때, HTML 내에 Blind라는 단어가 있거나, BLIND라는 단어가 있으면 두 경우 모두 해당된다.
• 검색어는 단어 단위로 비교하며, 단어와 완전히 일치하는 경우에만 기본 점수에 반영한다.
  • 단어는 알파벳을 제외한 다른 모든 문자로 구분한다.
  • 예를들어 검색어가 aba 일 때, abab abababa는 단어 단위로 일치하는게 없으니, 기본 점수는 0점이 된다.
  • 만약 검색어가 aba 라면, aba@aba aba는 단어 단위로 세개가 일치하므로, 기본 점수는 3점이다.
• 결과를 돌려줄때, 동일한 매칭점수를 가진 웹페이지가 여러 개라면 그중 index 번호가 가장 작은 것를 리턴한다
  • 즉, 웹페이지가 세개이고, 각각 매칭점수가 3,1,3 이라면 제일 적은 index 번호인 0을 리턴하면 된다.

접근 방법

문제를 해결하기 위해 크게 5가지 방법으로 나눌 수 있습니다.

1. 대문자를 모두 소문자로 전처리하기

2. 자신의 페이지 이름 파악하기

3. 페이지의 기본 점수 구하기

4. 자신의 페이지를 A, 외부로 나가는 링크를 B라 한다면 A에서 외부로 나가는 링크 B를 저장하고, B는 자신으로 들어오는 링크 A를 저장하기

5. 점수 구하기

일단 위의 과정을 설명하기 이전에 문제를 해결하기 위해 전역변수로 사용한 4개의 HashMap에 대해 설명하겠습니다.

1. map<int, string> name;  =>  name[페이지index] = "페이지 주소"
2. map<string, int> score;  =>  score[페이지 주소] = 기본 점수
3. map<string, vector<string>> outdegree; => outdegree["페이지 주소"] = {외부로 나가는 링크들}
4. map<string, vector<string>> indegree;  => indegree["페이지 주소"] = {자신으로 들어오는 외부 링크들}

1. 대문자를 모두 소문자로 전처리하기

아스키 코드 표를 사용하여 어렵지 않게 소문자로 변환할 수 있습니다.

void toSmall(string &page){
        
    for(int j=0;j<page.size();j++)
        if(65 <= int(page[j]) && int(page[j]) <= 90)
            page[j] = char(int(page[j]) + 32);       
}

2. 자신의 페이지 이름 파악하기

 string 헤더의 find함수를 적절히 사용하여 구할 수 있었습니다. 자신의 페이지 주소 뿐만 아니라 용도에 맞게 어떠한 페이지의 주소라도 파악할 수 있도록 pattern이라는 매개변수를 추가하였습니다.

만약 자신의 페이지 주소를 파악하기 위해서는 pattern = "<meta property=\"og:url\" content="가 될 것이며

외부로 링크의 페이지 주소를 파악하기 위해서는  pattern = "<a href=" 가 될 것입니다. 

(참고로 문자열 안에 "를 사용하려면 \를 붙여 사용할 수 있습니다.)

//string myNamePattern = "<meta property=\"og:url\" content=";
// string outLinkPattern = "<a href=";
string getLinks(string &page, string pattern, int &idx){
    
    string url = "";
    idx = page.find(pattern, idx);
    
    if(idx == string::npos) return url;
    else idx += pattern.size();
    
    while(page[++idx] != '"')
        url += page[idx];
    
    return url;
}

 이 함수는 찾아낸 페이지의 주소의 문자열을 반환하며, idx를 참조로 받아 동시에 페이지 주소가 끝나는 지점의 index로 갱신됩니다.

3. 기본점수 구하기

기본점수는 페이지 문서 내에서 해당 단어가 몇번 등장하는지 찾을 수 있습니다. 단어의 앞뒤에 영어 철자가 존재하면 안된다는 규칙이 있어 단어를 찾아낸 뒤에 단어의 시작 지점보다 한 칸 앞과 단어의 끝 지점의 한 칸 뒤를 모두 확인해야 합니다. 이 때 cnt는 페이지에서 찾은 word의 수 입니다.

int getScore(string &word, string &page){
    
    int idx = page.find(word);
    int cnt = 0;
    
    while(page.find(word, idx) != string::npos){ //단어를 찾을 수 있는 동안에
        
        bool isWord = true;
        idx = page.find(word, idx);
        
        //단어의 앞 부분 확인
        if(0 <= idx - 1 && idx - 1 < page.size() && 'a' <= page[idx - 1] && page[idx - 1] <= 'z')    
            isWord = false;
        //단어의 뒷 부분 확인
        if(0 <= idx + word.size() && idx + word.size() < page.size() && 'a' <= page[idx + word.size()] && page[idx + word.size()] <= 'z')    
            isWord = false;
        if(isWord)
            cnt++;
        idx += word.size();
    }
    return cnt;
}

4. 자신의 페이지를 A, 외부로 나가는 링크를 B라 한다면 A에서 외부로 나가는 링크 B를 저장하고, B는 자신으로 들어오는 링크 A를 저장하기

2번에서 설명한 getLinks 함수를 사용하여 while문으로 문서의 끝까지 외부로 나가는 링크가 있는지 탐색을 하여 hashmap인 indegree와 outdegree에 등록합니다.

pos = 0;
while(pos != string::npos){

	string link = getLinks(page, outLinkPattern, pos);
	if(link.size() == 0)
		break;

	outdegree[myName].push_back(link);
	indegree[link].push_back(myName);
}

5. 점수 구하기

이제 점수를 구하기 위한 모든 정보를 저장했습니다. 매칭 점수는 아래의 수식으로 구할 수 있습니다.

매칭 점수 = 자신의 기본점수 + (외부로 나가는 링크들의 '링크 점수')

링크 점수 = (링크의 기본점수/링크의 외부로 나가는 링크)

(참고로 여기서 자료형을 float을 사용하면 통과하지 못하는 테스트 케이스가 있었습니다.)

double getMatchScore(int idx){
    
    string myName = name[idx];
    
    double baseScore = double(score[myName]);
    
    double linkScore = 0;
    vector<string> inLinks = indegree[myName];
    for(int i=0;i<inLinks.size();i++){
        string link = inLinks[i];
        linkScore += (double(score[link]) / double(outdegree[link].size()));
    }
    return baseScore + linkScore;
}

소스 코드

#include <string>
#include <vector>
#include <map>

using namespace std;

map<int, string> name;
map<string, int> score;
map<string, vector<string>> outdegree;
map<string, vector<string>> indegree;

void toSmall(string &page){
        
    for(int j=0;j<page.size();j++)
        if(65 <= int(page[j]) && int(page[j]) <= 90)
            page[j] = char(int(page[j]) + 32);       
}

string getLinks(string &page, string pattern, int &idx){
    
    string url = "";
    idx = page.find(pattern, idx);
    
    if(idx == string::npos) return url;
    else idx += pattern.size();
    
    while(page[++idx] != '"')
        url += page[idx];
    
    return url;
}

int getScore(string &word, string &page){
    
    int idx = page.find(word);
    int cnt = 0;
    
    while(page.find(word, idx) != string::npos){
        
        bool isWord = true;
        idx = page.find(word, idx);
        
        if(0 <= idx - 1 && idx - 1 < page.size() && 'a' <= page[idx - 1] && page[idx - 1] <= 'z')    
            isWord = false;
        if(0 <= idx + word.size() && idx + word.size() < page.size() && 'a' <= page[idx + word.size()] && page[idx + word.size()] <= 'z')    
            isWord = false;
        if(isWord)
            cnt++;
        idx += word.size();
    }
    return cnt;
}
    
void processing(string &word, string &page, int idx){
    
    string myNamePattern = "<meta property=\"og:url\" content=";
    string outLinkPattern = "<a href=";
    
    int pos = 0;
    string myName = getLinks(page, myNamePattern, pos); //함수 내부에 참조연산자를 사용하여 pos가 변할 수 있음
    name.insert({idx, myName});
    
    int cnt = getScore(word, page);
    score.insert({myName, cnt});
    
    pos = 0;
    while(pos != string::npos){
        
        string link = getLinks(page, outLinkPattern, pos);
        if(link.size() == 0)
            break;
        
        outdegree[myName].push_back(link);
        indegree[link].push_back(myName);
    }
}

double getMatchScore(int idx){
    
    string myName = name[idx];
    
    double baseScore = double(score[myName]);
    
    double linkScore = 0;
    vector<string> inLinks = indegree[myName];
    for(int i=0;i<inLinks.size();i++){
        string link = inLinks[i];
        linkScore += (double(score[link]) / double(outdegree[link].size()));
    }
    return baseScore + linkScore;
}

int solution(string word, vector<string> pages) {
    
    int answer = 0;
    
    toSmall(word);
    for(int i=0;i<pages.size();i++)
        toSmall(pages[i]);
    
    for(int i=0;i<pages.size();i++)
        processing(word, pages[i], i);
    
    double maxScore = 0;
    for(int i=0;i<pages.size();i++){
        double nowScore = getMatchScore(i);
        if(maxScore < nowScore){
            maxScore = nowScore;
            answer = i;
        }
    }
    
    return answer;
}