문제 설명
카카오TV에서 유명한 크리에이터로 활동 중인 죠르디는 환경 단체로부터 자신의 가장 인기있는 동영상에 지구온난화의 심각성을 알리기 위한 공익광고를 넣어 달라는 요청을 받았습니다. 평소에 환경 문제에 관심을 가지고 있던 죠르디는 요청을 받아들였고 광고효과를 높이기 위해 시청자들이 가장 많이 보는 구간에 공익광고를 넣으려고 합니다. 죠르디는 시청자들이 해당 동영상의 어떤 구간을 재생했는 지 알 수 있는 재생구간 기록을 구했고, 해당 기록을 바탕으로 공익광고가 삽입될 최적의 위치를 고를 수 있었습니다.
참고로 광고는 재생 중인 동영상의 오른쪽 아래에서 원래 영상과 동시에 재생되는 PIP(Picture in Picture) 형태로 제공됩니다.

다음은 죠르디가 공익광고가 삽입될 최적의 위치를 고르는 과정을 그림으로 설명한 것입니다.
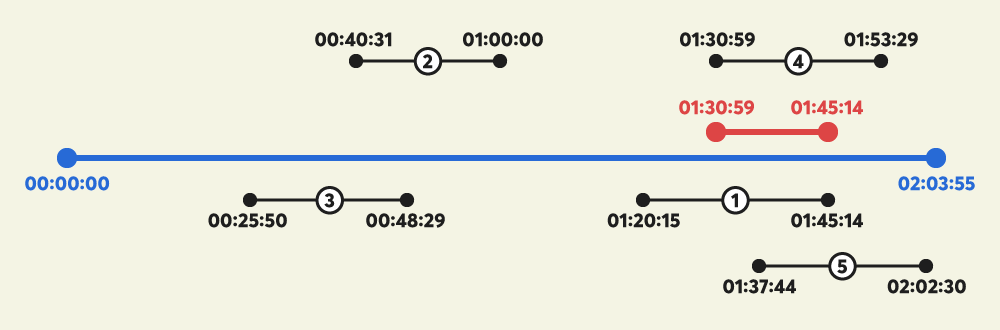
- 그림의 파란색 선은 광고를 검토 중인 죠르디 동영상의 전체 재생 구간을 나타냅니다.
- 위 그림에서, 죠르디 동영상의 총 재생시간은 02시간 03분 55초 입니다.
- 그림의 검은색 선들은 각 시청자들이 죠르디의 동영상을 재생한 구간의 위치를 표시하고 있습니다.
- 검은색 선의 가운데 숫자는 각 재생 기록을 구분하는 ID를 나타냅니다.
- 검은색 선에 표기된 왼쪽 끝 숫자와 오른쪽 끝 숫자는 시청자들이 재생한 동영상 구간의 시작 시각과 종료 시각을 나타냅니다.
- 위 그림에서, 3번 재생 기록은 00시 25분 50초 부터 00시 48분 29초 까지 총 00시간 22분 39초 동안 죠르디의 동영상을 재생했습니다. 1
- 위 그림에서, 1번 재생 기록은 01시 20분 15초 부터 01시 45분 14초 까지 총 00시간 24분 59초 동안 죠르디의 동영상을 재생했습니다.
- 그림의 빨간색 선은 죠르디가 선택한 최적의 공익광고 위치를 나타냅니다.
- 만약 공익광고의 재생시간이 00시간 14분 15초라면, 위의 그림처럼 01시 30분 59초 부터 01시 45분 14초 까지 공익광고를 삽입하는 것이 가장 좋습니다. 이 구간을 시청한 시청자들의 누적 재생시간이 가장 크기 때문입니다.
- 01시 30분 59초 부터 01시 45분 14초 까지의 누적 재생시간은 다음과 같이 계산됩니다.
- 01시 30분 59초 부터 01시 37분 44초 까지 : 4번, 1번 재생 기록이 두차례 있으므로 재생시간의 합은 00시간 06분 45초 X 2 = 00시간 13분 30초
- 01시 37분 44초 부터 01시 45분 14초 까지 : 4번, 1번, 5번 재생 기록이 세차례 있으므로 재생시간의 합은 00시간 07분 30초 X 3 = 00시간 22분 30초
- 따라서, 이 구간 시청자들의 누적 재생시간은 00시간 13분 30초 + 00시간 22분 30초 = 00시간 36분 00초입니다.
[문제]
죠르디의 동영상 재생시간 길이 play_time, 공익광고의 재생시간 길이 adv_time, 시청자들이 해당 동영상을 재생했던 구간 정보 logs가 매개변수로 주어질 때, 시청자들의 누적 재생시간이 가장 많이 나오는 곳에 공익광고를 삽입하려고 합니다. 이때, 공익광고가 들어갈 시작 시각을 구해서 return 하도록 solution 함수를 완성해주세요. 만약, 시청자들의 누적 재생시간이 가장 많은 곳이 여러 곳이라면, 그 중에서 가장 빠른 시작 시각을 return 하도록 합니다.
[제한사항]
- play_time, adv_time은 길이 8로 고정된 문자열입니다.
- play_time, adv_time은 HH:MM:SS 형식이며, 00:00:01 이상 99:59:59 이하입니다.
- 즉, 동영상 재생시간과 공익광고 재생시간은 00시간 00분 01초 이상 99시간 59분 59초 이하입니다.
- 공익광고 재생시간은 동영상 재생시간보다 짧거나 같게 주어집니다.
logs는 크기가 1 이상 300,000 이하인 문자열 배열입니다.
- logs 배열의 각 원소는 시청자의 재생 구간을 나타냅니다.
- logs 배열의 각 원소는 길이가 17로 고정된 문자열입니다.
- logs 배열의 각 원소는 H1:M1:S1-H2:M2:S2 형식입니다.
- H1:M1:S1은 동영상이 시작된 시각, H2:M2:S2는 동영상이 종료된 시각을 나타냅니다.
- H1:M1:S1는 H2:M2:S2보다 1초 이상 이전 시각으로 주어집니다.
- H1:M1:S1와 H2:M2:S2는 play_time 이내의 시각입니다.
시간을 나타내는 HH, H1, H2의 범위는 00~99, 분을 나타내는 MM, M1, M2의 범위는 00~59, 초를 나타내는 SS, S1, S2의 범위는 00~59까지 사용됩니다. 잘못된 시각은 입력으로 주어지지 않습니다. (예: 04:60:24, 11:12:78, 123:12:45 등)
return 값의 형식
- 공익광고를 삽입할 시각을 HH:MM:SS 형식의 8자리 문자열로 반환합니다.
[입출력 예]
play_timeadv_timelogsresult
| "02:03:55" | "00:14:15" | ["01:20:15-01:45:14", "00:40:31-01:00:00", "00:25:50-00:48:29", "01:30:59-01:53:29", "01:37:44-02:02:30"] | "01:30:59" |
| "99:59:59" | "25:00:00" | ["69:59:59-89:59:59", "01:00:00-21:00:00", "79:59:59-99:59:59", "11:00:00-31:00:00"] | "01:00:00" |
| "50:00:00" | "50:00:00" | ["15:36:51-38:21:49", "10:14:18-15:36:51", "38:21:49-42:51:45"] | "00:00:00" |
접근 방법
부분합과 투포인터를 적절히 사용하면 어렵지 않게 해결할 수 있는 문제였습니다.
접근 방법은 크게 4가지로 나눌 수 있습니다.
1. 시간정보에 관한 문자열을 초로 변환
2. arr[i]라는 배열을 i초에 보고 있던 시청자 수라 하였을 때, 1에서 변환된 초에 따라 arr배열에 기록
3. 광고를 0초부터 가능한 부분까지 1초씩 옮겨가며 arr배열의 정보를 사용하여 최댓값 갱신
4. 3에서 구한 값을 문자열로 변환
1. 시간정보에 관한 문자열을 초로 변환
문자열에서 ':'를 기준으로 for문을 통해 시간, 분, 초의 정보를 초로 변경하였습니다.
int string_to_sec(string time){
int sec = 0;
string sub = "";
for(int i=0;i<time.size();i++){
if(time[i] == ':'){
sec = (sec * 60) + (stoi(sub) * 60);
sub = "";
continue;
}
sub.push_back(time[i]);
}
sec += stoi(sub);
return sec;
}
2. arr[i]라는 배열을 i초에 보고 있던 시청자 수라 하였을 때, 1에서 변환된 초에 따라 arr배열에 기록
1번에서 설명한 string_to_sec()함수를 사용하여 문제의 입력으로 주어진 logs를 변환하여 arr[] 배열에 기록합니다.
for(int i=0;i<logs.size();i++){
int start = string_to_sec(logs[i].substr(0, 8));
int end = string_to_sec(logs[i].substr(9, 8));
for(int i = start;i<end;i++)
arr[i]++;
}
3. 광고를 0초부터 가능한 부분까지 1초씩 옮겨가며 arr배열의 정보를 사용하여 최댓값 갱신
광고시작시간이 0초일 때 시청자들의 누적 재생시간을 최대값의 초기값으로 설정하여 1초씩 시작시간을 증가시켜 최대값을 갱신합니다.
예를 들어 광고의 재생시간이 5초라고 한다면 sum1 = arr[0] + arr[1] + arr[2] + arr[3] + arr[4]가 될 것입니다. 이 때 광고의 시작시간을 1초 뒤로 옮기게 된다면 sum2 = arr[1] + arr[2] + arr[3] + arr[4] + arr[5]가 될 것입니다. 이 때 광고의 길이는 항상 일정하기 때문에 sum을 간단하게 구할 수 있습니다.
광고가 끝나는 시간을 i초, 광고의 길이를 a_time이라 하였을 때
sum(현재) = sum(과거) + arr[i] - arr[i - a_time]이라는 식을 유도할 수 있습니다.
즉 이전상태의 부분합을 안다면 다음상태에서 모든 요소를 참조하지 않고 현재상태의 부분합을 알아낼 수 있습니다.
//a_time은 광고길이, p_time은 영상길이
int accumulate(int a_time, int p_time){
long long maxsum = 0;
int result = 0;
for(int i=0;i<a_time;i++)
maxsum += arr[i];
long long sum = maxsum;
for(int i = a_time; i < p_time; i++){
sum += arr[i] - arr[i - a_time];
if(maxsum < sum) {
maxsum = sum;
result = i - a_time + 1;
}
}
return result;
}
4. 3에서 구한 값을 문자열로 변환
int형의 초를 60으로 나누어 가며 시, 분, 초로 변환을 하여 문자열을 구성을 합니다.
이 때 주의할 점은 시간은 60으로 나눈 나머지를 구해서 사용하면 안됩니다.(코드 복붙하다 여기서 틀린줄 모르고 많이 해맸음)
string sec_to_string(int sec){
string s = to_string(sec % 60);
if(s.size() == 1)
s = "0" + s;
sec /= 60;
string m = to_string(sec % 60);
if(m.size() == 1)
m = "0" + m;
sec /= 60;
string h = to_string(sec); //시간은 60으로 나눈 나머지를 사용하지 않는다.
if(h.size() == 1)
h = "0" + h;
return h + ":" + m + ":" + s;
}
소스 코드
#include <string>
#include <string.h>
#include <vector>
#include <iostream>
using namespace std;
int arr[360000];
int string_to_sec(string time){
int sec = 0;
string sub = "";
for(int i=0;i<time.size();i++){
if(time[i] == ':'){
sec = (sec * 60) + (stoi(sub) * 60);
sub = "";
continue;
}
sub.push_back(time[i]);
}
sec += stoi(sub);
return sec;
}
string sec_to_string(int sec){
string s = to_string(sec % 60);
if(s.size() == 1)
s = "0" + s;
sec /= 60;
string m = to_string(sec % 60);
if(m.size() == 1)
m = "0" + m;
sec /= 60;
string h = to_string(sec);
if(h.size() == 1)
h = "0" + h;
return h + ":" + m + ":" + s;
}
int accumulate(int a_time, int p_time){
long long maxsum = 0;
int result = 0;
for(int i=0;i<a_time;i++)
maxsum += arr[i];
long long sum = maxsum;
for(int i = a_time; i < p_time; i++){
sum += arr[i] - arr[i - a_time];
if(maxsum < sum) {
maxsum = sum;
result = i - a_time + 1;
}
}
return result;
}
string solution(string play_time, string adv_time, vector<string> logs) {
string answer = "";
int p_time = string_to_sec(play_time);
int a_time = string_to_sec(adv_time);
for(int i=0;i<logs.size();i++){
int start = string_to_sec(logs[i].substr(0, 8));
int end = string_to_sec(logs[i].substr(9, 8));
for(int i = start;i<end;i++)
arr[i]++;
}
int result = accumulate(a_time, p_time);
answer = sec_to_string(result);
return answer;
}'알고리즘 > 프로그래머스' 카테고리의 다른 글
| [C++, Java] 2021 카카오 블라인드 매출 하락 최소화 (0) | 2021.02.10 |
|---|---|
| [C++] 2021 카카오 블라인드 순위 검색 (0) | 2021.02.08 |
| [C++] 2021 카카오 블라인드 카드 짝 맞추기 (0) | 2021.02.05 |
| [C++] 2020 카카오 블라인드 기둥과 보 설치 (2) | 2021.02.03 |
| [C++] 2020 카카오 블라인드 가사 검색 (1) | 2021.02.03 |







